El Teorema de Descartes: Un Enigma de Siglos Finalmente Resuelto

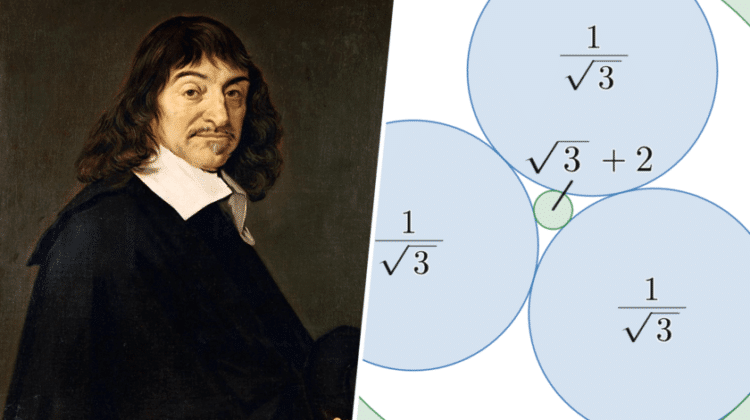
En 1643, René Descartes dirigió una carta a la princesa Isabel del Palatinado donde abordó un problema clásico de la geometría occidental, presentando una solución innovadora: el ‘teorema de Descartes’. Este teorema, popularizado más tarde cuando Frederick Soddy lo discutió en 1936 en la revista Nature, se puede resumir en que «la suma de los cuadrados de las cuatro curvaturas es la mitad del cuadrado de su suma en figuras».

Descartes logró encontrar una conexión entre los radios de cuatro círculos que se tocan entre sí. Sin embargo, el filósofo nunca explicó el razonamiento detrás de esta conexión ni logró formular una ecuación general para más de cuatro círculos, a pesar de su convicción de que debía existir una solución. Los matemáticos han estado trabajando en este problema desde entonces.

Recientemente, Daniel Mathews y Orion Zymaris, de la Universidad de Monash en Australia, adoptaron un enfoque completamente nuevo.

¿Qué pasaría si usamos herramientas de la física teórica? Esa fue la pregunta que se plantearon. En lugar de recurrir a la geometría convencional, utilizaron ‘espinores’, objetos de la física teórica que requieren un giro de 720 grados para regresar a su posición original.

«Empleamos una versión de espinores desarrollada por Roger Penrose y Wolfgang Rindler, quienes los aplicaron a la teoría de la relatividad», explicaron los investigadores. Este enfoque les permitió reconceptualizar los círculos como entidades algebraicas capaces de sufrir transformaciones geométricas.

Esta fue la clave para desarrollar una fórmula general que describe configuraciones cada vez más complejas de círculos que se tocan entre sí.

La importancia de este logro radica en su capacidad para resolver un problema histórico en geometría de una manera novedosa y con múltiples implicaciones.

Cuando Andrew Wiles demostró el último teorema de Fermat, algunos se sintieron decepcionados por el uso de herramientas matemáticas modernas. En ese caso, la gracia del problema era encontrar la demostración que Fermat afirmó haber descubierto (pero nunca documentó).

Con el teorema de Descartes la situación es diferente. No había una solución a la cual regresar, sino una oportunidad para desarrollar algo nuevo. Este logro destaca el potencial de las matemáticas para superar limitaciones que nos han restringido durante siglos.

Como bien expresó Arthur C. Clarke, «Cuando un científico distinguido pero de edad avanzada afirma que algo es posible, es casi seguro que tiene razón. Cuando afirma que algo es imposible, es casi seguro que está equivocado.»

Imagen | Frans Hals | Jacob Rus